Animated Experiment:

Introduction

As can be seen from the animated tensile experiment, the first phase of the stress-strain diagram for a typical ductile material is completely elastic. At any load level within the elastic phase, upon release of the load the strain is totally recovered. This is the implication of elasticity. Depending on the specimen material, the linear elastic range may or may not be followed by a short non-linear elastic phase. That is, linear elasticity generally dominates the elastic behavior of ductile specimens.

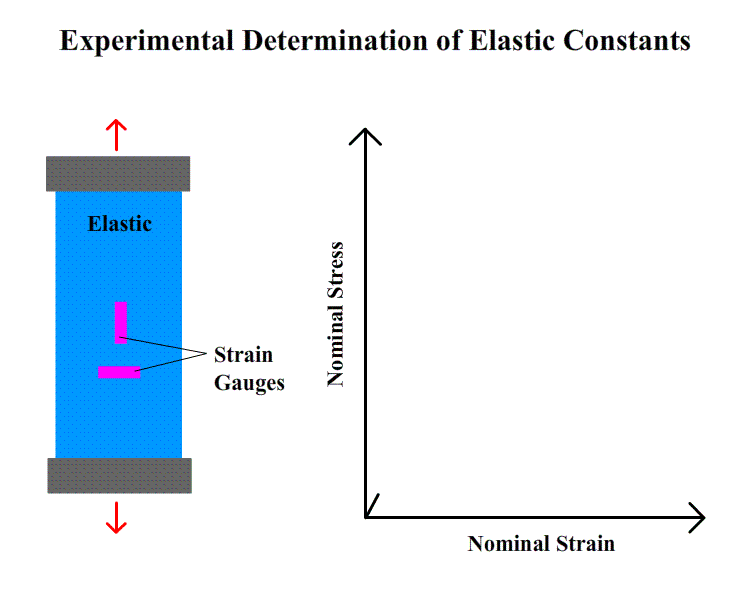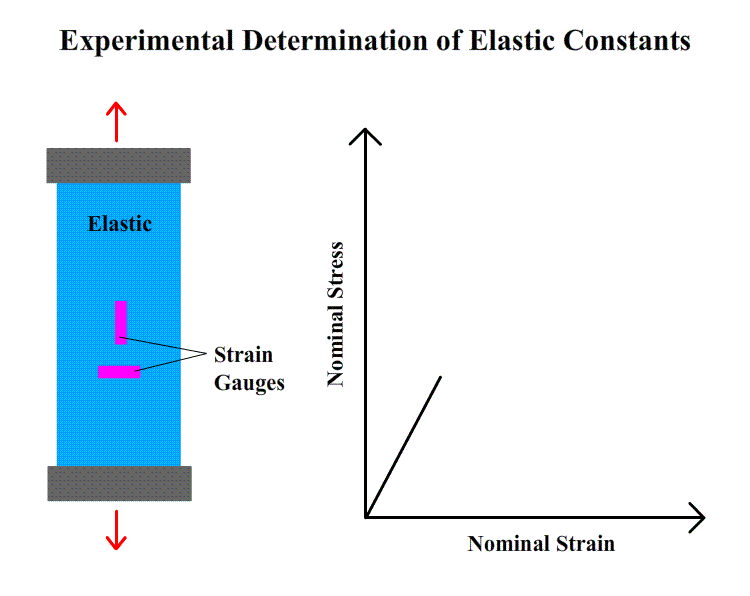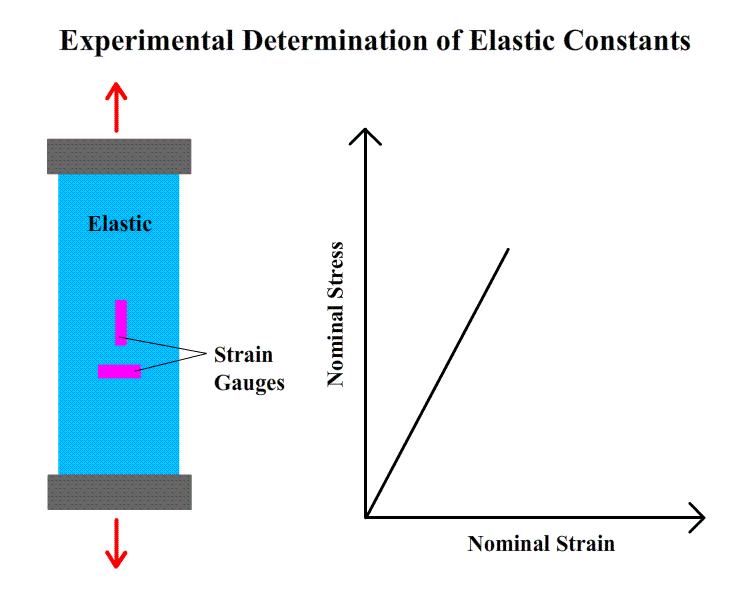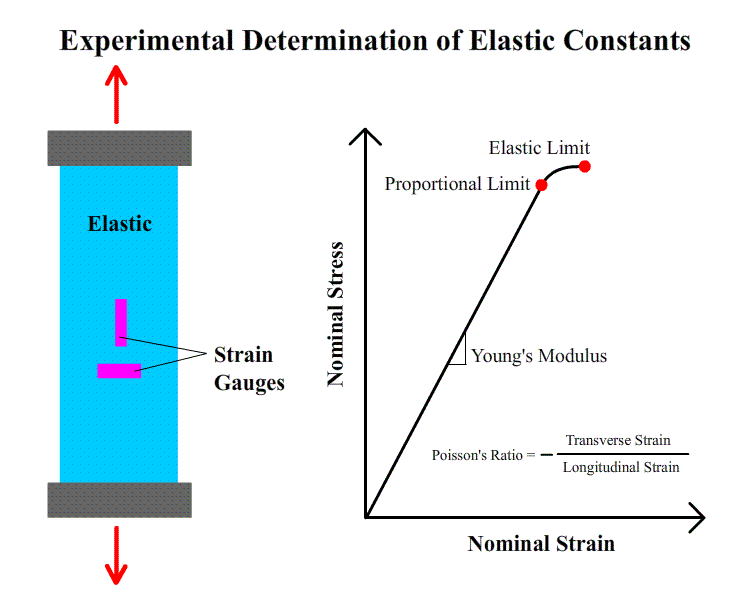
There are three important parameters that define the linear elastic behavior of a ductile material, namely Young’s modulus, proportional limit and Poisson’s ratio. Young’s modulus, often also referred to as modulus of elasticity, is simply the slope of the linear portion of the stress-strain curve. In other words, it is defined as the ratio of the stress (force per unit area) along an axis over the strain (ratio of deformation over initial length) along that axis in the range of stress in which Hooke's law holds. It is named after the 19th-century British scientist Thomas Young and is a measure of the stiffness of an elastic material. Do not confuse rigidity and strength: the strength of material is characterized by its yield strength and / or its tensile strength.

The proportional limit is the largest tensile stress that a specimen can support in the linear stress-strain relationship.

Poisson's ratio, named after Siméon Poisson, is the negative ratio of transverse to axial strain. If a structural element is stretched along one direction, it usually tends to contract in the directions transverse to the direction of stretching. This is a common observation when a rubber band is stretched, when it becomes noticeably thinner. The Poisson’s ratio will be the ratio of relative contraction to relative expansion. In certain rare cases, a material will actually shrink in the transverse direction when compressed (or expand when stretched) which will yield a negative value of the Poisson ratio.

For brittle materials (e.g., gray cast iron, concrete, and many polymers) this elastic portion of the stress–strain curve is typically not linear; hence, it is not possible to determine a modulus of elasticity as described above. For this nonlinear behavior, either tangent or secant modulus is normally used. Tangent modulus is taken as the slope of the stress–strain curve at some specified level of stress (e.g. the proportional limit), while secant modulus represents the slope of a secant drawn from the origin to some given point (e.g. the elastic limit) of the stress-strain curve.

Principle

The experimental determination of Young’s modulus and the proportional limit has been demonstrated in the tensile experiment. No new information other than the nominal stress-strain curve is required. The determination of Poisson’s ratio, however, must be facilitated by strain gauges. This is obvious from its definition. Both the longitudinal and transverse deformation of the linear phase must be measured. As illustrated in the animated diagram, two strain gauges are needed; one is attached transversely and the other longitudinally. Their negative ratio yields Poisson’s ratio. Visit the principle of strain gauge page on this site for more information about strain measurements.

Objective

Determine Young’s modulus, proportional limit and Poisson’s ratio of a typical ductile material.

Apparatus

See tensile experiment.

Procedure

See tensile experiment. Note that only the linear phase of the nominal stress-strain curve is necessary for the determination of Young’s modulus and proportional limit. Poisson’s ratio is simply determined from the reading of strain gauges at each load increment.

Quiz

- Why is it necessary to apply longitudinal strain gauges on both sides of the specimen?

- How to eliminate the adverse influence on measurements due to possible bending deformation?

- How to analyze the measurement uncertainty of elastic constants?

- Explain the tangent and secant method that are used for determining the elastic constants of brittle specimens.

Further Reading

- Hooke’s Law http://en.wikipedia.org/wiki/Hooke%27s_law

- Young’s Modulus http://en.wikipedia.org/wiki/Young%27s_modulus

- Poisson’s Ratio http://en.wikipedia.org/wiki/Poisson%27s_ratio

- Elastic Modulus http://en.wikipedia.org/wiki/Elastic_modulus